DP: 한 문제를 해결하기 위해 문제를 부분 문제로 분할하여 해결하고 부분문제들의 해를 바탕으로 큰 문제를 해결하는 문제해결기법.
정의를 딱 보자마자 생각나는 생각이 분할정복이랑 비슷하다라는 생각이 든다. 하지만 내용은 문제를 나눈다는 사실을 제외하고는 비슷한 문제해결방법이 아니다. 심지어 문제를 나누는 것도 분할정복은 큰 문제라는 덩어리를 여러부분으로 쪼개는 느낌이고, DP는 큰 문제의 이전 단계의 경우를 생각하는 걸 문제를 나눈다고 한다.
분할정복: 큰 덩어리 문제를 작은 덩어리로 쪼개서 해결한 뒤에 합치는 방식으로 문제를 해결
DP : 큰 문제를 작은 부분 문제로 나누고 작은 부분 문제의 해을 저장하여 중복 계산을 피하거나, 작은 부분문제의 최적해로 점화식을 세워 큰 문제를 해결
DP는 문제 유형을 2가지로 분류할 수 있다.
1. 중복 부분 문제: 큰 문제를 작은 부분 문제로 나누고, 작은 부분 문제의 해결책을 저장하여 중복 계산을 피한다. Memoization 또는 Tabulation을 통해 중복 부분 문제를 해결한다.
- Memoization: Top-down 방식으로 큰 문제에 먼저 접근하여 큰 문제를 해결하기 위해 하위 단계의 문제에 접근하면서 하위 단계의 해가 구해지면 Dp_table에 저장하는 형식이다. 예를 들어, dp[4]를 구하기 위해 dp[4]를 구하기 위해선 dp[3]이 필요하고 dp[3]을 구하기 위해서 dp[2],...dp[1] 이 필요하다는 식으로 접근하여 기저사례(base case)에 도달하면 다시 재귀적으로 dp[1],dp[2],dp[3]에 값이 저장되어 dp[4]가 구해지는 방식(보통 재귀로 구현)
2. 최적 부분 구조 문제: 큰 문제의 최적해가 작은 문제의 최적해를 통해서 구해지는 경우. 큰 문제를 작은 문제로 나누고 나눈 작은 문제의 최적해를 통해서 큰 문제의 해를 구하는 방식. Memoization 또는 Tabulation을 통해 중복 부분 문제를 효과적으로 해결한다.
- Tabulation: Buttom up 방식에서 도표, 표 등을 작성하는 방식을 말한다. 예를 들어, dp[4]를 구하기 위해 필요한 이전 단계의 문제를 생각하지 않고 바로 dp[1],dp[2],dp[3]을 구해서 dp[4]를 구하는 방식.
본인이 글을 잘쓰는 편도 아니고 당연히 글만으로는 이해가 어려우니 각각의 경우에 대해 예시를 통해서 설명을 이어나가겠다.
1. 이항계수(중복 부분 문제 예시)
https://www.acmicpc.net/problem/11051
11051번: 이항 계수 2
첫째 줄에 \(N\)과 \(K\)가 주어진다. (1 ≤ \(N\) ≤ 1,000, 0 ≤ \(K\) ≤ \(N\))
www.acmicpc.net
이항계수는 이항정리를 하였을때의 계수이며, 순서없는 조합의 가짓수 이다.
다음의 성질을 확통에서 배웠을 것이다. 아래의 성질을 다이나믹 프로그래밍에 적용하여 이항계수를 빠르게 구할 수 있다.
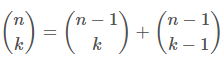
Top-down 메모이제이션으로 이항계수를 구해보자.

위에서 설명했듯이 중복 부분 문제는 큰 문제로 바로 접근하여 큰 문제를 해결하기 위해 필요한 작은 문제들을 재귀형태로 구현한다.
그림과 같이 계속해서 내려가다가 k == 0 이거나 n == k 이 되면 1을 리턴해주면 된다.(nC0, nCn은 1이므로 기저사례)
하지만 단순 재귀로만 구현하면 중복 되는 문제를 여러번 계산하기 때문에 TLE가 발생할 것이다. 이를 위해 우리는 특정 n,k에 대한 조합값이 구해질 때마다 똑같은 조합을 두 번 이상 계산하지 않기 위해 값을 캐시배열에 저장을 해놓았다가 꺼내 쓸 것이다.
구상도에서 볼 수 있듯이 2단계 밖에 안했음에도 불구하고 벌써 bio(n-2,k-1)이 두 번 중복해서 나오는 것을 확인할 수 있다.
코드로는 다음과 같이 작성할 수 있다.
#include <iostream>
#include <cstring>
using namespace std;
// 값을 저장할 캐시 배열
int cache[1001][1001];
// Top-down Dp
int bino(int n, int k){
// base case 세팅.
if(k==0 || n==k) return cache[n][k] = 1;
// 현재 캐시 배열의 값을 참조
int &ret = cache[n][k];
// 배열에 초기화 값이 아닌 작은 부분 문제의 값이 들어있으면 바로 꺼내씀.
if(ret != -1) return ret;
// 재귀로 값을 구하면서 캐시 배열에 구한 값을 저장해놓음.
return cache[n][k] = (bino(n-1,k) + bino(n-1,k-1))%10007;
}
// 값을 입력받고 캐시 배열 초기화
int main(){
int n,k,ans;
cin >> n >> k;
memset(cache,-1,sizeof(cache));
bino(n,k);
cout << cache[n][k];
}
2. 동전 문제(최적 부분 구조 문제 예시)
https://www.acmicpc.net/problem/2293
2293번: 동전 1
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
www.acmicpc.net
동전의 개수와 가치가 나와있고 적당히 잘 조합하여 동전가치의 합이 K원이 되도록 하는 경우의 수를 묻는 문제이다.
문제를 Top-down으로 구상하자면 할수는 있겠지만 Buttom-up이 더 쉬울거 같다.
바로 dp[k]에 접근하는 것이 아닌 dp[1]부터 순서대로 쌓아가며 dp[k]까지 도달하는 방식이다. 최적 부분 구조 문제들은 점화식을 세우기가 좀 까다로울 수 있는데 작은 문제의 최적해가 큰 문제의 최적해와 어떻게 연관이 있을지 고민해봐야한다.
1원과 2원을 사용해서 5원을 만드는 경우를 생각해보자. (dp[n]은 n원을 만드는 경우의 수)
맨처음 1원만 사용할 때는 당연히 dp[1] = 1, dp[2] = 1, dp[3] = 1, dp[4] = 1, dp[5] = 1이 될 것이다.
1원과 2원을 동시에 사용할 때는
1원을 만드는 경우, 변화가 없으므로 dp[1] = 1
2원을 만드는 경우, 기존 1원만 사용해서 2원을 만드는 경우 + 0원에서 2원짜리 1개를 사용해 2원을 만드는 경우 (dp[2] = dp[2] + dp[2-2] = 2)
3원을 만드는 경우, 기존 1원만 사용해서 3원을 만드는 경우 + (1원과 2원을 모두 사용해)1원을 만드는 경우에서 2원짜리 1개를 사용해 3원을 만드는 경우 (dp[3] = dp[3] + dp[3-2] = 2)
4원을 만드는 경우, 기존 1원만 사용해서 4원을 만드는 경우 + (1원과 2원을 모두 사용해) 2원을 만드는 경우에서 2원짜리 1개를 사용해 4원을 만드는 경우 (dp[4] = dp[4] + dp[4-2] = 3)
5원을 만드는 경우, 기존 1원만 사용해서 5원을 만드는 경우 + (1원과 2원을 모두 사용해) 3원을 만드는 경우에서 2원짜리 1개를 사용해 5원을 만드는 경우 (dp[5] = dp[5] + dp[5-2] = 3)
위와 같이 해서 최종적으로 1원과 2원을 모두 사용해서 5원을 만드는 경우를 구할 수 있다.
마지막 부분 dp[5]에서 1원 + 2원짜리를 2개 사용하는 경우를 왜 고려안하냐고 할 수있는데, dp[3]을 구할 때 이미 2원짜리를 고려해서 구했기 때문에 이미 dp[3]에 포함되어 있다.
처음에 보면 낯설고 많이 어색할 수 있지만 연습만이 살길이라고 많은 연습을 필요로 하는 문제 유형이다.
위의 예시를 일반화하여 코드를 작성하면 다음과 같다.
#include <iostream>
#include <algorithm>
#include <vector>
#define endl "\n"
using namespace std;
int main() {
int n,k; cin >> n >> k;
// 동전의 종류를 담을 배열
int coin[101];
// 동전의 종류 입력받기
for(int i=0;i<n;i++){
cin >> coin[i];
}
// 메모이제이션을 할 배열 생성 및 초기화
int dp[10001] = {0,};
// 기저사례(base case)
dp[0]=1;
for(int i=0;i<n;i++){
for(int j=coin[i];j<=k;j++){
// 큰 문제의 최적해를 작은 문제들의 최적해로 구함.
dp[j] = dp[j] + dp[j-coin[i]];
}
}
cout << dp[k];
}다이나믹 프로그래밍은 초심자가 시작할 때 마주치는 첫번째 고비이다. 대회는 물론이고 코딩테스트에서도 출제 빈도가 높기 때문에 많은 연습을 통해서 감을 익혀야 한다.
DP를 하면서 많이 하는 질문들이 Top-down으로 풀어야하는지 Buttom-up으로 풀어야하는지가 있다. 대부분의 문제는 두 방법모두 사용해서 풀 수는 있지만 대게 특정방법이 간단하게 풀리는 경우가 많다. Top-down 방식으로 사고하는 연습이 dp실력을 늘리는데 중요기 때문에 우선 Top-down으로 생각해본 후에 점화식이 잘 안보이면 buttom-up으로 고민해보는 것이 좋다. Top-down은 보통 재귀로 구현하므로 당연히 재귀 개념이 잡혀있지 않으면 힘들기 때문에 연습하고 Dp로 넘어오는 것을 추천한다.
연습이 많이 필요한 문제해결방법이기에 꾸준한 문제풀이만이 답이다.
'📚알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| Constructive 관찰(1) (1) | 2024.12.08 |
|---|---|
| 그리디 알고리즘(Greedy) (0) | 2024.11.25 |
| 분할정복(Divide and Conquer) (6) | 2023.12.19 |
| 스택 & 큐(Stack and Queue) (1) | 2023.12.18 |
| 이분 탐색(Binary Search) (2) | 2023.12.18 |
