● 분할정복(Divide and Conquer)
한번에 해결하기에 불가능하거나 매우 오래걸리는 문제를 작은 문제로 나눠서(분할) 해결하고 다시 결합하여(정복) 문제를 해결하는 방식
**앞서 포스팅 했던 이분탐색 또한 분할정복을 사용한 알고리즘
Merge sort(병합정렬)
분할정복을 이용한 정렬방법으로 O(NlogN)의 시간복잡도를 가지며 버블정렬, 삽입정렬, 선택정렬 보다 실행시간이 빠르다. (파이썬에 내장되있는 sort함수도 병합정렬)
병합정렬을 통해서 분할정복이 어떤식으로 이루어지는지 알아보자.
정렬을 하기 위해 임의의 무작위 배열 arr = [3, 25, 1, 75, 42, 100, 63, 38] 이 있다고 하자. 이 배열의 Divide 과정은 아래그림과 같다.

배열의 중간을 기준으로 더 이상 나눌수 없을 때까지 계속하여 나누어 주었다. 이제 Conquer를 하면서 문제를 해결해나가야 하는데 우리의 목적은 정렬이므로 정렬하면서 나눈 배열을 다시 합친다.
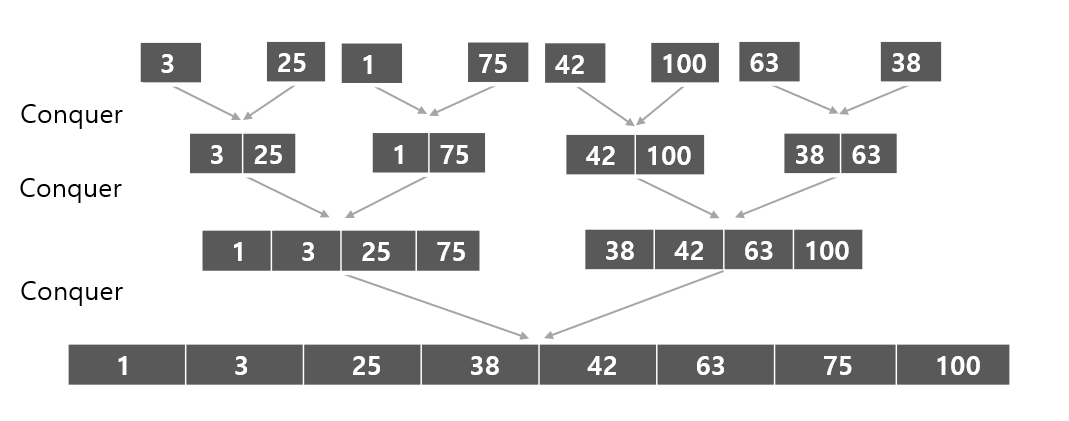
정렬하면서 다시 원래 배열로 합치는 과정이다.
정렬하는 과정은 나눠진 배열의 첫번째에 포인터를 둬서 합치는 배열의 포인터를 비교하는 방식으로 해나간다.
두번째 Conquer과정을 예시로 들면,
3과 1비교 ([1]) -> 3과 75비교 ([1, 3]) - > 25와 75비교 ([1, 3, 25]) -> 75 ([1, 3, 25, 75])
42와 38비교 ([38]) -> 42와 63비교([38, 42]) -> 63과 100 비교 ([38, 42, 63]) -> 100 ([38, 42, 63, 100)]
분할된 배열의 첫번째 위치에 포인터를 두고 포인터에 위치한 수가 합쳐질 때마다 포인터를 뒤로 하나씩 밀면 된다.
결국 더 효율적으로 정렬하기 위해 분할정복을 한 것이므로 시간복잡도가 어떻게 줄어들었는지 확인해보자.
버블정렬, 선택정렬, 삽입정렬의 최악의 시간복잡도는 O(n²)이다.
<병합정렬의 시간복잡도>
정렬하는데 필요한 n개의 원소와 logN번의 과정이 있으므로 O(NlogN)의 시간복잡도를 가진다.
정확히는 배열을 복사하고 나누는 과정 때문에 NlogN의 상수배일 것이지만 상수배는 무시할수 있으므로 Big-O Notation은 O(NlogN)이 된다. 분할정복을 사용했더니 직관적으로 수행할 수 있는 정렬(버블,선택,삽입)들 보다 효율적인 시간복잡도가 나왔다. 이로써 큰 문제를 다룰때는 작은 문제로 분할하여 해결한 후 다시 합치는 분할정복 기법을 사용하는 것이 효율적임을 알 수 있다.
Merge sort이외에도 c++라이브러리에서 지원하는 퀵 정렬, 큰 수의 거듭제곱 등은 분할정복을 사용하면 효율적으로 해결할 수 있는 문제들이다.
특히 큰 수의 거듭제곱은 분할정복을 통해서 얼마나 시간을 줄일 수 있는지 꼭 직접 해보는 것을 추천한다.
https://www.acmicpc.net/problem/1629
1629번: 곱셈
첫째 줄에 A, B, C가 빈 칸을 사이에 두고 순서대로 주어진다. A, B, C는 모두 2,147,483,647 이하의 자연수이다.
www.acmicpc.net
분할정복을 이용한 거듭제곱 문제이다.
분할정복은 Merge sort와 같이 전부다 다시 합치는 경우도 있고, 필요한 부분만 골라서 합칠 수도 있어 문제를 해결하는데 다양하게 사용될 수 있다.
'📚알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| 그리디 알고리즘(Greedy) (0) | 2024.11.25 |
|---|---|
| 동적 계획법(Dynamic Programming) (1) | 2023.12.23 |
| 스택 & 큐(Stack and Queue) (1) | 2023.12.18 |
| 이분 탐색(Binary Search) (2) | 2023.12.18 |
| 완전 탐색(Brute-force Search) (1) | 2023.12.18 |
