어떤 코드가 잘 짠 코드이고, 어떤 코드가 못짠 코드일까?
코드의 가독성, 메모리, 시간 등 여러 요소가 있겠지만 그중에서 효율성(시간)에 관련된 빅오 표기법에 대해 쓰려한다.
● Big-O Notation
정의는 다음과 같다.
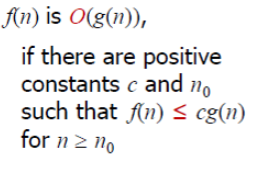

전공서적에 있는 것을 그대로 옮긴 것인데, 해석한 그대로이다.
n이 n0 보다 큰 경우에서 어떠한 양의 정수 c를 g(n)에 곱해도 함숫값이 f(n)보다 크거나 같은 경우 함수f(n)의 시간복잡도를 O(g(n))이라고 한다.
다시말하면, 어떤 알고리즘의 실행시간이 f(n)을 따라간다고 할때 그 알고리즘은 적어도 cg(n)보다는 빠른 시간에 작동된다는 뜻이다.
예를 들어,
- f(n) = 5n²+3n+7는 O( n²)
- f(n) = 6n+1은 O(n)
- f(n) = 8n³+2n² + 9n + 2 는 O( n³)
의 시간복잡도를 가진다
눈치가 빠른분들은 정의의 마지막 줄에서 눈치챘겠지만 함수 식의 최고차항이 핵심이다.
n과 n²을 비교해보자. f(n) = n이 f(n) = n²보다 큰 경우가 있다고 한들 결국 n0(1>=) 이후로는 전부 n²의 값이 더 크다는 것을 알 수 있다.
따라서 코드의 Big-O Notation은 최고차항이 결정한다.
간단하게는 2중 반복문(for,while)이면 n², 3중이면 n³ ... 으로 생각하면 편하지만 내장함수의 시간복잡도까지 곱해주어야한다.
만약 2중 for문 안에 max함수 등을 사용하면 max,min 함수는 배열 전체를 선형적으로 탐색해서 가장 큰 것을 찾기 때문에 시간복잡도가 O(n)이다.
따라서 전체 시간복잡도는 n² (2중for문) * n(내장함수) = O( n³)이 된다.
// n²의 시간복잡도
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
//....
}
}
// n³의 시간복잡도
for(int i = 0; i < n; i++){
for(int j = 0; j < n; j++){
int tmp = *max_element(arr);
//.....
}
}
같은 기능을 하는 코드라면 당연히 Big-O Notation의 차수가 낮을 수록 효율적인 코드이다. 코드의 효율성은 간단한 데이터로는 체감이 어렵지만, 데이터가 방대해질 수록 차이가 드러난다. 심하면 하루종일 실행시켜야 결과가 나오는 코드가 1초안에 나오게 할 수도 있으니 말이다.
대표적으로 이분탐색의 시간복잡도는 O(logN) 이다. 단순하게 선형적으로 탐색하면 O(n)이 나오므로 선형탐색보다 효율적인 시간복잡도를 가지는 알고리즘이다.
Merge sort나 quick sort는 파이썬과 c++ 의 내장함수로 있는 정렬로 평균적으로 O(NlogN)의 시간복잡도를 가진다.
'📚알고리즘 > 알고리즘 이론' 카테고리의 다른 글
| 동적 계획법(Dynamic Programming) (1) | 2023.12.23 |
|---|---|
| 분할정복(Divide and Conquer) (6) | 2023.12.19 |
| 스택 & 큐(Stack and Queue) (1) | 2023.12.18 |
| 이분 탐색(Binary Search) (2) | 2023.12.18 |
| 완전 탐색(Brute-force Search) (1) | 2023.12.18 |
